This past Summer, I took advantage of the free Coursera membership that the University of Minnesota granted all of their students by enrolling in Princeton’s Algorithms course. The first assignment is titled Percolation, and was one of my favorite assignments to complete in the course.
The project was described as follows (Sedgewick & Wayne, 2008):
Write a program to estimate the value of the percolation threshold via Monte Carlo simulation.
Percolation. Given a composite systems comprised of randomly distributed insulating and metallic materials: what fraction of the materials need to be metallic so that the composite system is an electrical conductor?
The model. We model a percolation system using an n-by-n grid of sites Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of adjacent open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row.
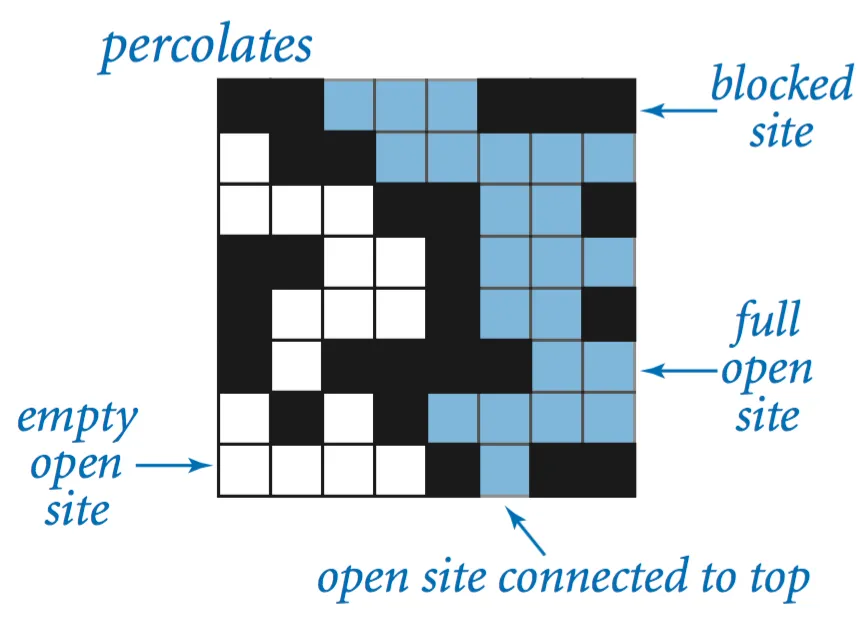
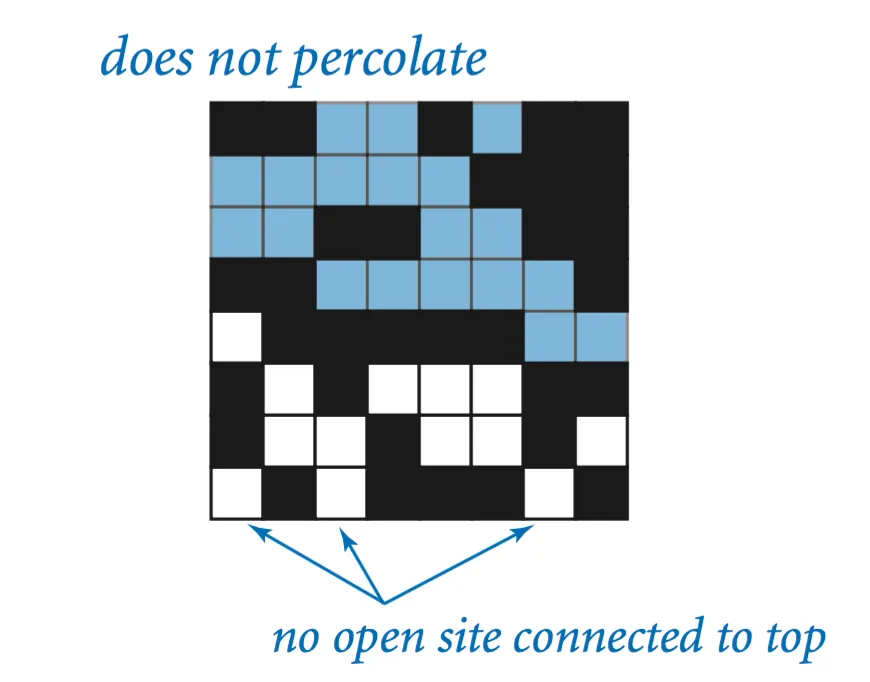
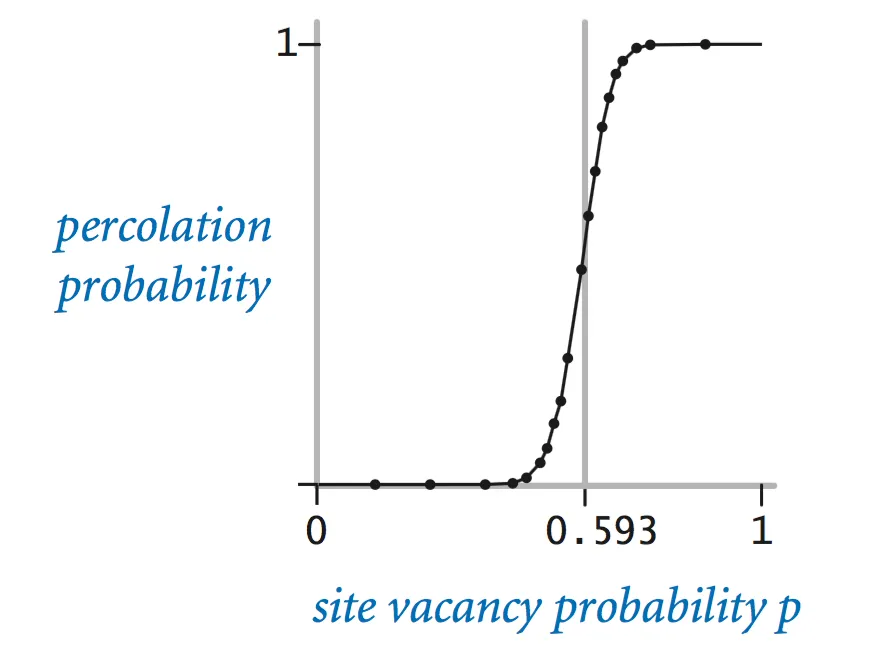
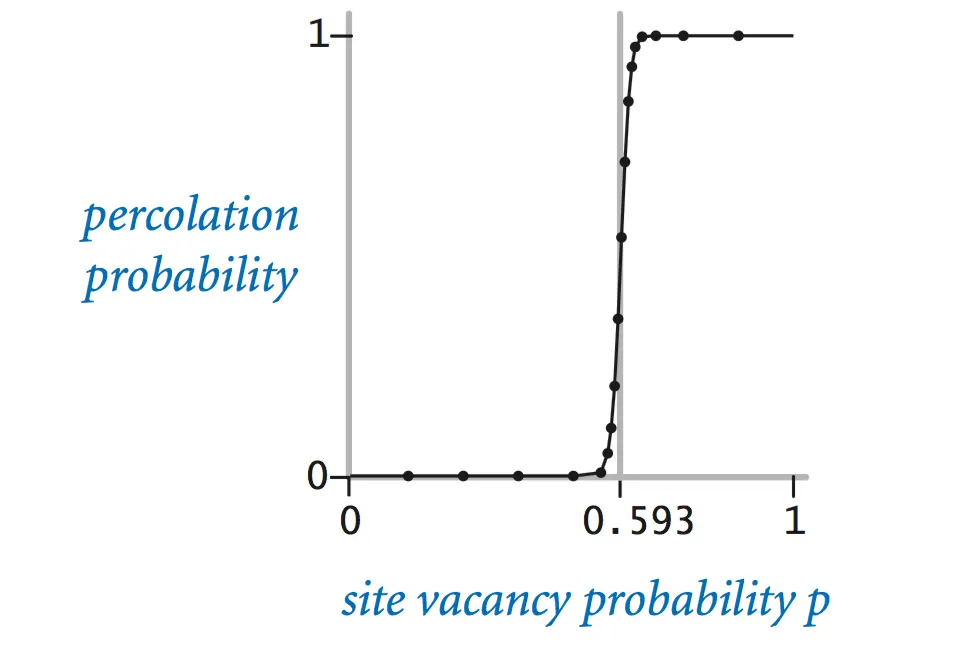
The problem. In a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p, what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20-by-20 random grid (left) and 100-by-100 random grid (right).
Tasks
To complete this assignment, I was tasked with developing the Percolation and PercolationStats Java classes.
The Percolation class represents a n-by-n grid containing sites that are either closed, open, or full (open and connected to any of the top row sites).
The PercolationStats class in conjunction with the Percolation class can be used to perform monte carlo simulations to determine the percolation threshold. The percolation threshold is defined as the probability of site openness in which if you have a higher percent of sites open than the threshold, you can be almost certain that the grid percolates. Conversely, if the percent of open sites is below the percolation threshold, you can be almost certain that the grid doesn’t percolate.
A Monte Carlo simulation in this context operates as follows:
- Initialize all sites to be blocked.
- Repeat the following until the system percolates.
- Choose a site uniformly at random among all blocked sites.
- Open the site.
- The fraction of sites that are opened when the system percolates provides an estimate of the percolation threshold.
These steps are repeated for many instances of the same grid so that sample statistics can be produced, such as mean average, standard deviation, and 95% confidence intervals.
Approach
To keep tabs on the state of the grid system, a Union-Find data structure was used. Union-Find data structures are useful for many applications involving dynamic connectivity such as social networks and metallic sites in a composite system.
My solution used two Union-Find structures to determine whether the system was percolating. The first Union-Find structure used contained $ N * N + 2 $ nodes. The $ N * N $ component accounts for all the squares in the grid system, while the accounts for two virtual sites. One of the virtual sites is connected to all of the top row grid sites upon construction, and the other virtual site is connected to all of the bottom row grid sites similarly.
As the sites open up and a top element has a path to the bottom element, the top virtual site will be connected to the bottom virtual site. Once this connection is made, we know that the system percolates without having to check every single top/bottom row element. Since we only need to check the top/bottom virtual site to determine percolation, the program completes this operation in $ O(1) $ time instead of $ O(N) $ time.
The second Union-Find structure used contained $ N * N + 1 $ nodes, and was only used to determine if a specific site was full (connected to any of the top row elements).
Challenges
During the development of the Percolation class, it became evident that there was an issue with determining whether a bottom site was full or not after a Percolation object had percolated. This issue stemmed from the virtual bottom site that would detect whether percolation had occurred. After percolation, the bottom site would make all the bottom sites (and any sites connected to said bottom sites) appear to be full, even if they had no connection to the top virtual element.
This challenge was solved by creating a second WeightedQuickUnionUF object that was solely responsible for determining whether any site was full or empty.
Assessment Summary
Princeton’s Algorithms course on Coursera has an auto grader that will test your program against a plethora of test files that test edge-case. Below is the assessment of my code:
- Compilation: PASSED
- API: PASSED
- Spotbugs: PASSED
- PMD: PASSED
- Checkstyle: FAILED (0 errors, 11 warnings)
- Correctness: 32/33 tests passed
- Memory: 8/8 tests passed
- Timing: 20/20 tests passed
- Aggregate score: 98.18%
Failed Correctness Test Report
Test 16: check for backwash with predetermined sites
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
OperationCountLimitExceededException
Number of calls to methods in WeightedQuickUnionUF exceeds limit: 250000000
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
==> FAILED
The reason this test fails is because my implementation of the Percolation class implements two WeightedQuickUnionUF objects. Because of this, the calls to methods of WeightedQuickUnionUF objects is roughly double.
Memory Analysis
Percolation: $ 17n^2 + 288 $ bytes
PercolationStats: $ 48 $ bytes
A bonus test conducted by the auto grader states that if a students implementation uses $ 11n^2 + 128n + 1024 $ bytes of memory or less, then the student will receive bonus points towards the aggregate score. I assume this would be achieved if my implementation used just one WeightedQuickUnionUF object.